Select Cluster from the main menu:

The cluster dialog opens up:
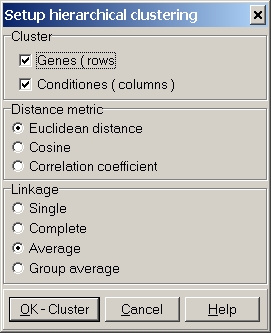
Define the parameters used for clustering:
Select to cluster Genes and/or Conditions (=Hybridizations).
Clustering may be performed in one go, or you can first cluster genes, then
cluster conditions with different distance metric or linkage.
Several distance metrics may be selected. See below for more details about the metrics.
At present three linkage methods may be selected (Group average does not work yet). See below for more details about the metrics.
Run clustering algorithm with specified parameters.
A progress indicator box will show up.
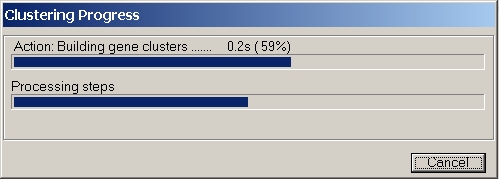
The lower progress indicator bar shows the main processing steps:
The upper progress indicator bar shows the progress of each of the (up-to) four steps.
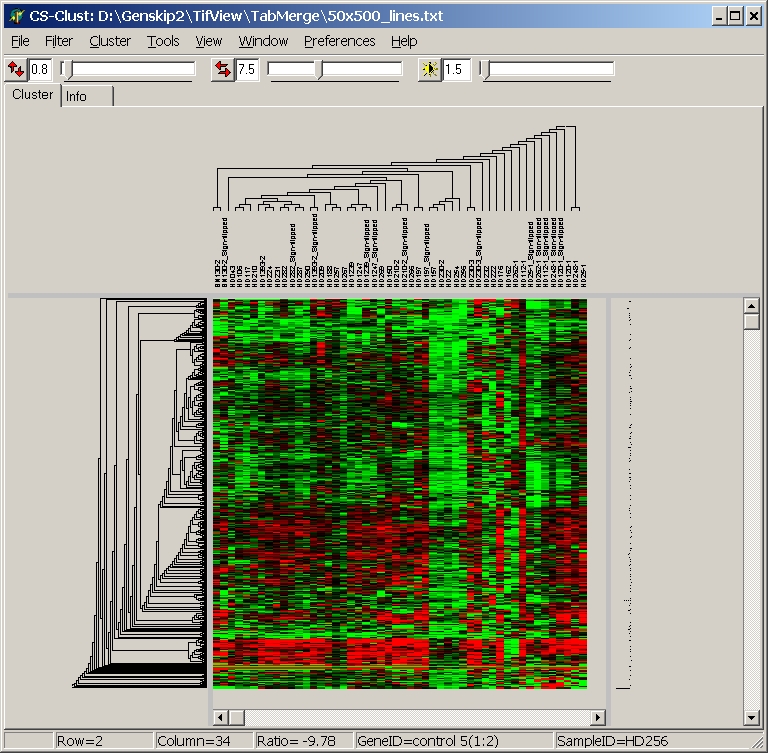
After clustering, the heatmap view will update and show the computed trees:
| 1. | d(x,y) ≥ 0 | non negativity |
| 2. | d(x,y) = d(y,x) | symmetry |
| 3. | d(x,x) = 0 | identity |
| 4. | d(x,y) = 0, if and only if x = y | definiteness |
| 5. | d(x,z) ≤ d(x,y) + d(y,z) | triangle inequation |
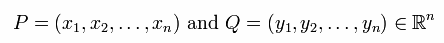
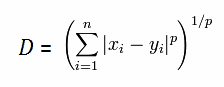
| Lets look at a very simple example in two dimensional space (n=2): | 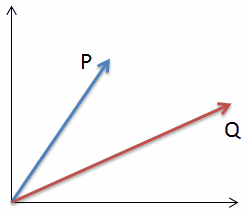 |
| Manhattan distance (p=1): | 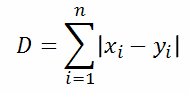 | 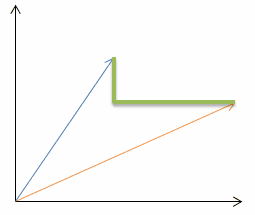 |
| Euclidean distance (p=2): | 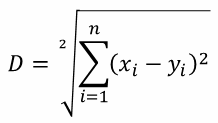 | 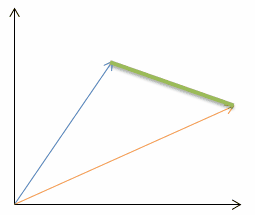 |
| Chebyshev distance (p=infinite): | 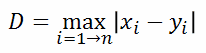 | 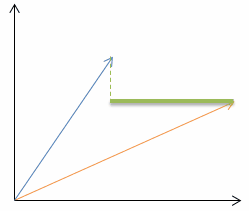 |
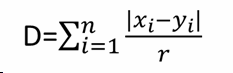 with r = n
with r = n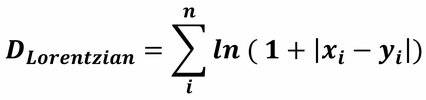
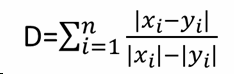
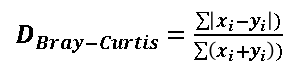
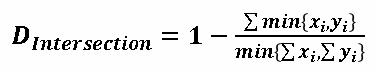
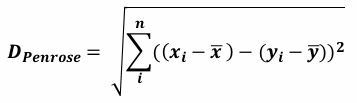
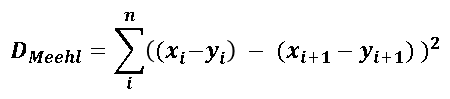
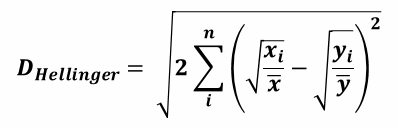
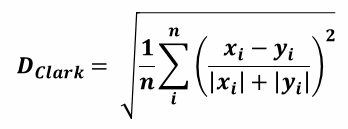
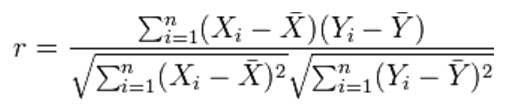
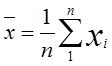
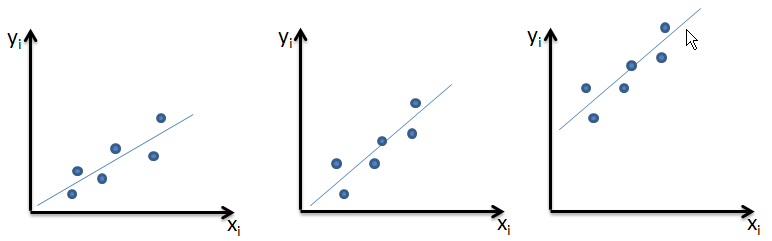
| 1 = | identical shape of vectors |  |
| 0 = | no similarity in vector's shape |  |
| -1 = | complete opposite shape of the vectors |  |
| P | 4 | 2 | 10 | 6 | 8 |
| Q | 5 | 3 | 42 | 20 | 40 |
| P | 4 | 2 | 10 | 6 | 8 |
| Ranks(P) | 2 | 1 | 5 | 3 | 4 |
| Q | 5 | 3 | 42 | 20 | 40 |
| Ranks(Q) | 2 | 1 | 5 | 3 | 4 |
| Ranks(P) | 2 | 1 | 5 | 3 | 4 |
| Ranks(Q) | 2 | 1 | 5 | 3 | 4 |
| P | 4 | 2 | 10 | 6 | 8 |
| Q | 5 | 20 | 42 | 40 | 3 |
| P | 4 | 2 | 10 | 6 | 8 |
| Ranks(P) | 2 | 1 | 5 | 3 | 4 |
| Q | 5 | 20 | 42 | 40 | 3 |
| Ranks(Q) | 2 | 3 | 5 | 4 | 1 |
| A | B | C | D | E | |
| Ranks(P) | 2 | 1 | 5 | 3 | 4 |
| Ranks(Q) | 2 | 3 | 5 | 4 | 1 |
| Pair | Data | concordant | dis-concordant |
| A-B | 2 > 1 2 < 3 | X | |
| A-C | 2 < 5 2 < 5 | X | |
| A-D | 2 < 3 2 < 4 | X | |
| A-E | 2 < 4 2 > 1 | X | |
| B-C | 1 < 5 3 < 5 | X | |
| B-D | 1 < 3 3 < 4 | X | |
| B-E | 1 < 4 3 > 1 | X | |
| C-D | 5 > 3 5 < 4 | X | |
| C-E | 5 > 4 5 < 1 | X | |
| D-E | 3 < 4 4 > 1 | X | |
| Sum | 6 | 4 |
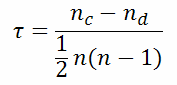 | ||
| with | nc=number of concordant pairs | |
| nd=number of disconcordant pairs) | ||
| n=dimension of data vectors | ||
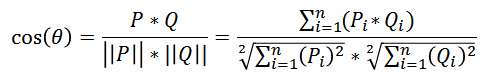 |
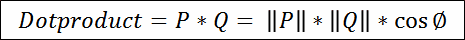 |
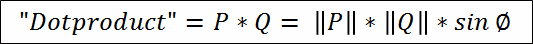 |
| n11 | number of common existing elements in both vectors ("1" - "1").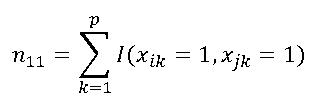 In the example: xi = ( 1,1,0,1,0,0,1,1,0,1,0,1 ) xj = ( 1,0,1,1,0,1,1,0,0,0,1,1 ) n11= 4 | |
| n00 | number of common missing elements in both vectors ("0" - "0").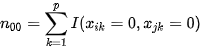 In the example: xi = ( 1,1,0,1,0,0,1,1,0,1,0,1 ) xj = ( 1,0,1,1,0,1,1,0,0,0,1,1) n00= 2 | |
| n10 | number of elements only exisitng in first vector ("1" - "0") .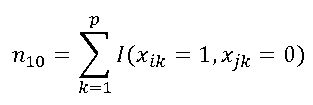 In the example: xi = ( 1,1,0,1,0,0,1,1,0,1,0,1 ) xj = ( 1,0,1,1,0,1,1,0,0,0,1,1 ) n10= 3 | |
| n01 | number of elements only exisitng in second vector ("0" - "1")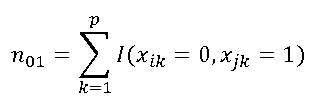 In the example: xi = ( 1,1,0,1,0,0,1,1,0,1,0,1 ) xj = ( 1,0,1,1,0,1,1,0,0,0,1,1 ) n01= 3 |