Non negative Matrix Factorization (NMF)

Genome wide molecular analysis (e.g. gene expression ~30000 features), mehthylation (~450000 features)of hundreds samples results in huge datasets wich are not easy to inspect or interpret.
Dimensionalty reduction techniques may help to simplify data interpretaion while keeping the underlying patterns / forces.

Non negative Matrix Factorization (NMF) tries to express the complex source matrix as a product of two matrices with much lower dimensionalty:

W_i,j = W_i,r x H_r,j

With R= Rank of the factorization (r<<i and r<&t;j).

E.g.: Factorizing a complete geneExpression data set with r=2 would operate with matrices like:
Dimensionalty of V: ~30000x500
Dimensionalty of W: ~30000x2
Dimensionalty of H: ~2x500

The property on non negativity allows to apply a straight forward updating-rule based algorithm to find a solution for the factorization.
Algorithms for Non-negative Matrix Factorization Daniel D. Lee, H. Sebastian Seung
Advances in Neural Information Processing Systems 13 edited by T.K. Leen and T.G. Dietterich and V. Tresp.
proceedings from the conference, "Neural Information Processing Systems 2000.
In an iterative way, W and H are recomputed.
Due to the update function and non-negative values, the iteration will converge to a stable solution of NMF.
A cost function is used to estimate the monotonic decreasing difference between V and W x H after each iteration.

The extracted simplified matrices W and H can be used to assign conditions (samples) to classes defined by the derived meta-features (genes) in H, as well as to assign features (genes) to classes defined by derived meta-conditons (samples in) W.

The high dimensonalty of source and even result data, lead to the fact, that multiple (similar) approximative solutions for the factorization exist.

The most suited assignment of conditions/features may be found when running multiple randomly initialized factorization runs.
From all runs the pairwise co-assignments of conditions/features is collected in a consensus similarity matrix.
The matrix may be sorted (clustered) to visualize underlying structure of the factorization.

Like with any other clustering approach, remove data which are not supportive:

non annotated features
low abundant features
data measured at detection limit will not drive information und thus wil mask/hide or dilute the underlying patterns
low variance data
constant data can not help to deduced underlying patterns
...

Best, reduce the starting data matrix to a few thousand rows/columns to enable fast and efficient analysis.

NMF with SUMO

From the main tool bar select Clustering | NMF | NMF:

a parameter dialog opens up.
Define how to perform NMF:

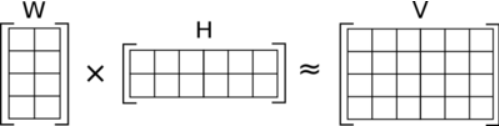
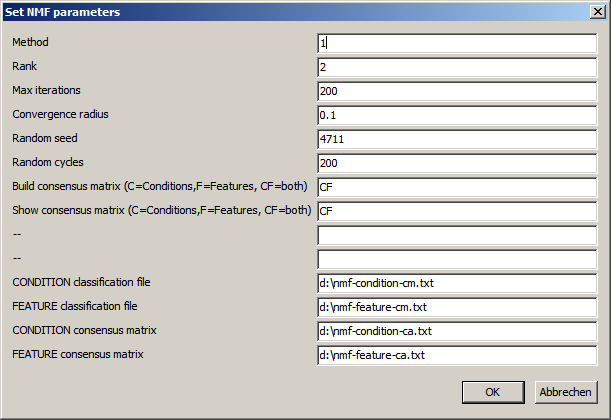
Method	Define how the iterative is performed. 1=Lee, Seung: Multiplicative update with Educledean distance as cost function 2=Lee, Seung: Multiplicative update with Kullback-Leibler divergence as cost function ...
Rank	Number of factors for Conditions/features Should be a small number (2..10..) Give a range (e.g. "2,5") to run 4 complete rounds of NMF. Starting with NMF rank=2, followed by NMF rank=3, .... Result files are generated with a tag defining the rank (e.g. *_r2.txt for all results from NMF with rank=2)
Max. iterations	Maximumn number of iterations to perform in a single NMF run In case the NMF problem can not be solved the process might run infinitely. After user defned maximumn number of iteratons the update process is interrupted independent of convergence.
Convergence radius	After each update cycle, the relative change of the cost function is computed. The cost function should assymptotically approach Zero (but probably never reach it). Define the maximal accepted change (in %) of the cost funcion to stop the updating, harvesting a close approximation to a solution of NMF. As smaller the convergence radus as better the approximated solution, and as more update loops are required
Random seed	W and H are initialized with random numbers. Define a fixed start value to ensure the same sequence of random numbers. This may be hepful, to compare diffrent NMF runs with varying parameters. Leave the field empty for completely random sequences.
Random cycles	Number of NMF cycles with different randomly initialized W and H matrices. Condition/Feature associations to factors are collected and will be used to build a consensus similarity matrix.
Build consensus matrix C: only for the conditons F: only for features CF: both empty: none	Factor asignments for condtitons/features are collected after each random cylce and saved in the condition-/feature factor file. Additionally you may build the consensus similartity matrix and save it (condition & feature consensus matrix). Building of consensus matrices becomes time consuming (dim > 10000) and requires a lot of memory which may crash the program (dim > 35000). Thus, you may only build one (the smaller) matrix, or build the matrix later, independently reusing the condition-/feature factor files.
Show consensus matrix C: only for the conditons F: only for features CF: both empty: none	Having build the consensus similarity matrix, you may immediately show data in a heatmap viewer. With matrices dim > 20000 this may crash *SUMO*.
Files	Base names for result files. *SUMO* will use the base names to store results from the different randomization rounds at the specified location. (e.g. "d:\nmf_Condition_cm_r1.txt" as consensus similarity matrix for ramdom round 1.

Click OK-button to run NMF.

Specified number of Random cycles NMF are performned. For each rond, W and H matrix are intitalized with a new set of random numbers (in the same numerical range as data matrix V).
Update iterations are run until relative change of cost function falls belowe user defined convergence radius or user defined max number of iterations is reached.
Next all Conditons are assigned to feature factors:
For each conditon, all "meta features" are checked.
The respective condition is assign to the meta-feature with highest numerical values.
Same procedure is applied to assign features to meta conditions.
Conditon/feature asignment to factors is saved using user defined file names.
If requested, consensus similarity matrices are generated and saved.
If requersted, consensus matrices are sown as heatmap views.

Computation progress is shown and summarized in Log tab-sheet and status bar:

For each random round, basic results are shown:

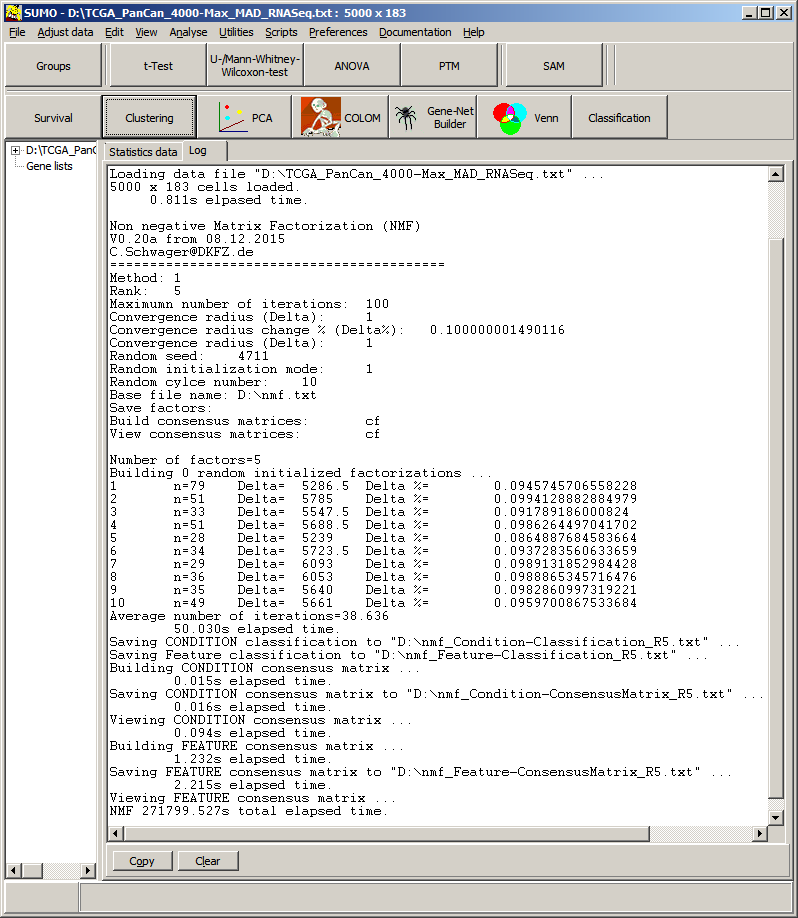
#	Number of random round (e.g. 1=first round)
n	Number of iterations in this round. (e.g. 94 iterations for round 1, if n equals user defined number of max iterations, NMF didn't reach user defined accuracy. May be adjust parameters and run again.
Delta	Value of cost functions at last performed round. Delta=abs(Costfunction[i-1]-Costfunction[i];
Delta %	Relative change of cost function between secod last and last random round. Delta%=(Delta / CostFunction[i-1])*100; Here, cost function changed between last two random rounds by ~0.097%. This is smaller user defined convergence radius => stop iterative update scheme and finalize randoum round 1.

Next name of created result files and some timings are shown.

Timings / performance:
NMF update scheme runs in linear time and linear memory consumption.
Consensus matrices require sqared time and memory consumption.

Some Timings (I7, 1 thread, 2.6GHz, rank=5, 100 random cycles, delta%=0.1):

Features (Rows)	Conditions (Columns)	of iterations	t NMF (s)	Condition matrix t (s)	Save C-CM t (s)	Feature matrix t (s)	Save F-CM t (s)	Total t (s)
100	100	120	0.047	0.015	0.187	0.016	0.016	14.820
200	100	105	24.134	0.047	0.015	0.016	0.016	24.695
500	100	101	55.458	0.047	0.016	0.031	0.047	56.004
1000	100	106	115.113	0.063	0.015	0.109	0.156	115.878
2000	100	107	231.568	0.063	0.016	0.873	0.578	233.643
5000	100	104	565.020	0.109	0.015	6.489	3.526	576.080
10000	100	103	1432.183	0.172	0.015	30.763	14.337	1480.060
15000	100	104	2094.563	0.219	0.015	75.255	31.887	2207.351