Dimensional reduction - PCA / tSNE / UMAP

Microarrays measure levels of thousands of mRNAs or proteins in dozens or hundreds of samples ( e.g. different growth conditions for cell cultures, blood samples from patients, ...). Data can be interpreted as  hundreds or thousands conditions (samples ) in thousands-dimensional gene vector space (factors).
Such high-dimensionality makes visualization of samples difficult and limits simple exploration and interpretation of data.

Therefore, dimensionality reduction techniques try to summarize and project the high dimensial information into a few dimensions 1-/2-/3D space allowing to analyze conveniently overall data structure.


Principal Component Analysis (PCA) is a mathematical algorithm that reduces the dimensionality of the data while retaining most of the variation in the data set. I.e. model large pairwise distances between the data vectors.

t-distributed Stochastic Neighbor Embedding (t-SNE) is an alternative method to model the small pairwise distances which may be better suited to visually explore the data and find clusters of similar objects.

Uniform Manifold Approximation and Projection for Dimension Reduction (UMAP) is an other method for low dimensional embedding, simliar to t-SNE but with probably higher processing speed and probably better visualization.










PCA

It accomplishes this reduction by identifying "directions" in the high dimensional factor-space, called principal components, along which the variation in the data is maximal.
By using the first few principal components, which will contain most information to distinguis the analysed samples, and showing them in a 2/3-dimensional scatterplot, it will be facilitated to distinguish similar groups in the analyzed data set and correlate these groups to sample annotations.

Assume an example:
You would like to group students at a University. Beyond others you may record size, weight, size of shoes, ..., hair colour, eye colour, skin colour, ...
Obviously there are some close correlation between some of the parameters:
Tall people mostly have larger shoes and higher weight, often people with blonde hair have blue or green eyes and bright skin.
Thus it might be useful to define combined principal properties (e.g. "Size").

Mathematical concept

When mining a dataset comprised of numerous factors, (used interchangeably with the term dimensions hereinafter), it is likely that subsets of factors are highly correlated with each other. Given a high correlation between two or more factors it can be concluded that these factors are quite redundant thus share the same driving principle in defining the outcome of interest.
In multivariate datasets, dimension reduction by PCA enables us to analyze our data in a visible 2-dimensional (2D) or 3D space, with only a mere loss of information.

The following steps are performed:<
1. Computation of the covariance and correlation matrix.
All pair wise correlations values between any pair of factors (factor-Number=N) is computed, resulting in a square NxN matrix .
2.  Finding of N Eigen-values and N Eigen-vectors for the correlation matrix.
This is a basic mathematical operation, with the aim to find a system of orthogonal base-vectors spanning the  NxN dimensional space of the matrix in such a way, that the 1. Eigen-vector contains most variance (=information) to describe the data set.
The system is solved with the Jacobi algorithm. This is a iterative system, which may  - or may not - converge to a stable solution. Convergence criterium is measured whether the difference between two consecutive iteration-cycles falls below a predefinedthreshold (convergence radius).
If a stable solution can be computed, a valid solution of PCA is found, if not - there might be certain reasons:
Anyway, the last most accurate solution (within the exit criteria) is presented.

3. Sorting Eigen-values / Eigen-vectors, with decreasing Eigen-value.
4. Adjust Eigen-vectors to have 1. element >0
5. z-transform covariance matrix, i.e. scale covariance matrix columns in such a way that columns have Mean=0 and Standard deviation=1
6. Compute projection of observables on first few (typically first three) Eigen-vectors.
7. Compute correlation-matrix  between factors and Eigen-vectors.
NB:
As larger the number of factors as more computational problems.
Memory requirements grow squared with number of factors: 14,000 genes would already require ~4 GByte of memory to store the matrices.
Iterative solution of the >1000 dimensional Eigen-vector system may never converge simply due to computational accuracy.
NB:

For more details about PCA see:
What is principal component analysis? Ringner M. Nat Biotechnol. 2008 Mar;26(3):303-4.
Jaakko Hollmen's  introduction to principle component analysis





PCA with SUMO

Click the PCA button from SUMO's toolbar:


Select to perform PCA with


With Genes as factors all genes are used.

With Conditions as factors group selector shows up and allows to select a subset of conditions to perform PCA with:


On the parameters page the parameters for calculating PCA may be adjusted:

NB: Oly change parameters if you now what you are doing !!


Click the Run button to perform PCA.

A new node is added to the analysis tree:

>Parameter: View defined parameters and general analysis results:










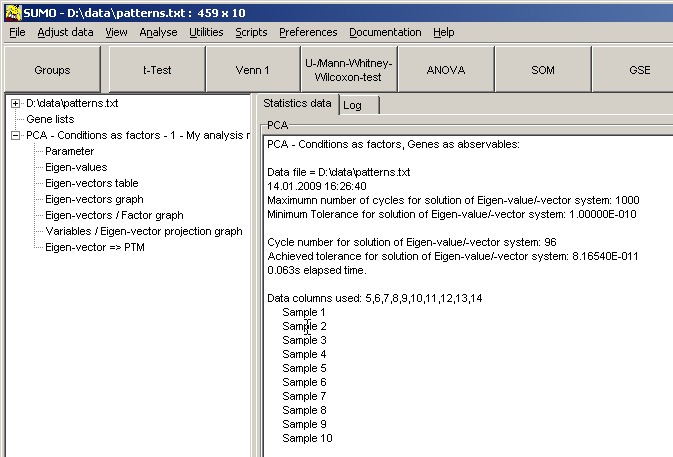
tSNE


tSNE computes internally a two dimensional probabilty distribution map of pairwise vector similarities.
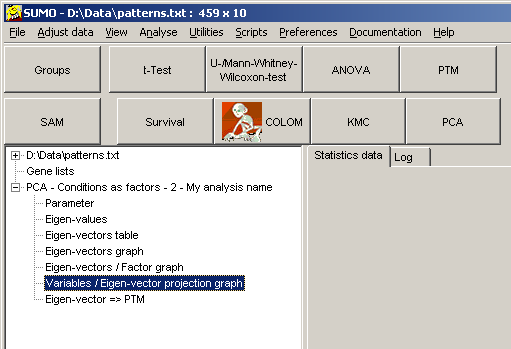
A output 2D map - the tSNE-graph - is generated.
In an iterative process, the data points on the output map are moved to minimize the Kullback-Leibler divergence between these two maps.
t-SNE may be better suited to model the small pairwise distances betweeen data vactors and thus may be better to visually explore the result data and find structure / clusters of similar objects.
On the other hand, the neighbour embedding does not necessarily reflect real magnitude of similarity between individual data points / clusters.
Therefore, tSNE-maps should be compared with other "embedding" techniques (e.g. PCA, clsutering).

For more details about tSNE see L.J.P. van der Maaten and G.E. Hinton. Visualizing High-Dimensional Data Using t-SNE. Journal of Machine Learning Research 9(Nov):2579-2605, 2008.

or a basic introduction into t-SNE; Paper Dissected: "Visualizing Data using t-SNE" Explained.

SUMO does not use an own implementation of tSNE but utilizes the improved FFT-accelerated Interpolation-based t-SNE (FIt-SNE) version implemented by Linderman et al. (2017).
To ensure compatibility, SUMO uses "FItSNE-Windows-1.0.0", from Dec-2018, downloaded from their web-site and mirrored on SUMO web site.



t-SNE with SUMO

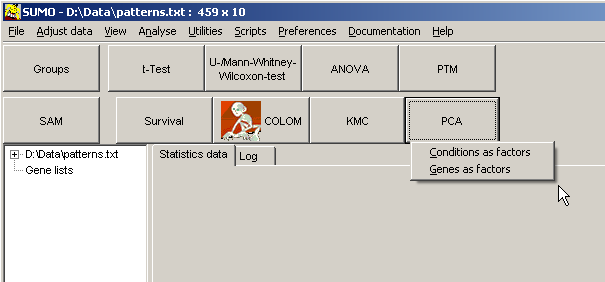
Load a data matrix.

Click the PCA / t-SNE-button or select Main menu | Analyses | PCA / t-SNE.

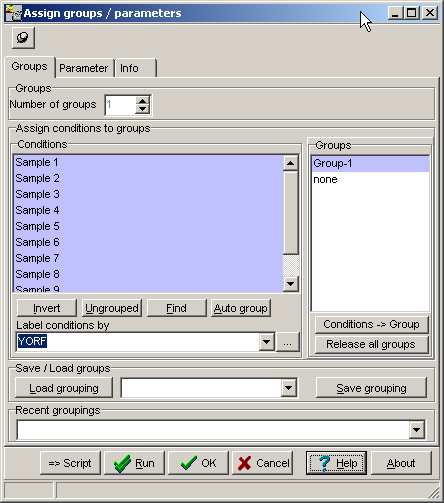
Select to run a t-SNE analysis with either Genes (row-vectors) or Conditions (column vectors).

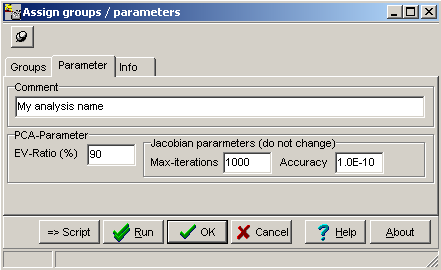
A parameter dialog opens up, allowing to set of few FItSNE processing parameters:

Max number of
iteration cylces     		 Number of cycles, FItSNE tries to optimize positioning the output vectors.
A larger number of iteration may generate a more accurate map, in case FItSNE finds a local optimal solution.
Most simply, run FItSNE with a decent number of iterations (e.g. 250).
In case the mapping looks non informative, try to run it again with more iterations (e.g. 500 next round 100, ...).
Better, run FItSNE on the command line and see its progress dependong on the iterations.
Perplexity: A larger perplexity will tend to spread the data clouds.
Try different values and observe the outcome.
But: recommended Perplexity = (Number_of_Features_Conditions - 1) / 3).
I..e. 30 samples => Perplexity ~10.
SUMO automatically adjusts a too high perplexity accordingly.
Dimensions:' Generate a 2 dimensional embedding => data clouds in a 2d-plain (commonly used model)
or a 1-dimensional embedding => stacked bars

SUMO generates a FIt-SNE specific data file, saves it in the folder where SUMO executable reside, und starts FItSNE.

FItSNE requires numeric data - obvious.
Thus, you should impute non-numeric values in your data matrix prior to running FItSNE.
In case /SUMO finds non numeric values while writing the FItSNE data file, it will finally replace NANs by ZERO.
In case of very few randomly distributed NAN cells, this will most probably not interfere with the mapping.
Larger number of NANs concentrated in singular data rows/columns or even correlating with data structures may introduce biases and thus artificial mappings.

Depending on data size (i.e. number of data vectors, length of data vectors) and internal data structure, FItSNE may require a while to process the data.

Some timings with random data, I7-3930, 3GHZ, 12 hyperthreads, 32 GB RAM:

Number of   
vectors		Legth of   
vectors		Consumed   
RAM
(GB)		Elapsed   
time
(s)
10000010002.8270
1000010000.330
100010000.0315
1000100000.345
10001000002.565

Thus, be patient and wait until FIt-SNE has finalized.
Although in principle possible, it may be wise not to run other SUMO functionality while waiting for FIt-SNE.

You may terminate FIt-SNE by clicking the Break button or press ESC-key.

As soon as FIt-SNE has finalized, SUMO will pick up FIt-SNE binary result file.
It converts and stores result data into a tab-delimited text file ("SUMO-path\fitsne.txt) which may be used anywhere.
The tab-delimited text file contains the mapping coordinates in the first two data columns, as well as feature/sample annotation in the third columns (multiple annotation separated by ";".

Furthermore, SUMO shows FIt-SNE mapping in it's Scatterplot viewer:



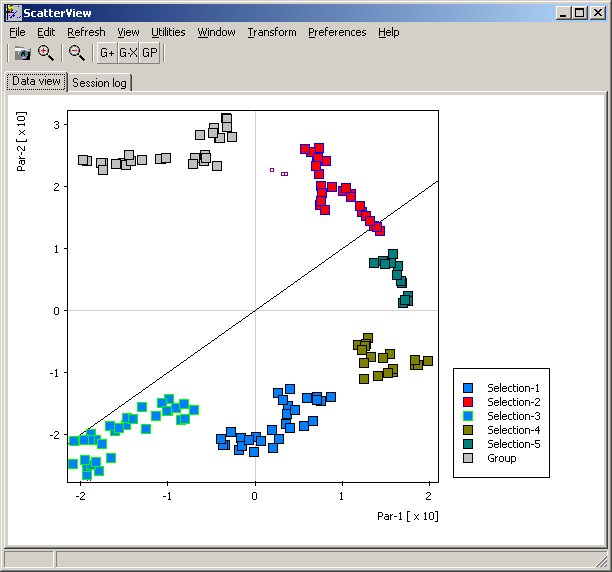
All annotatins are passed to the Scatterplot viewer too.


Thus you may search for certain data (Scatterplot main menu | Find) or draw selection ROIs and review contained data points and their annotations:




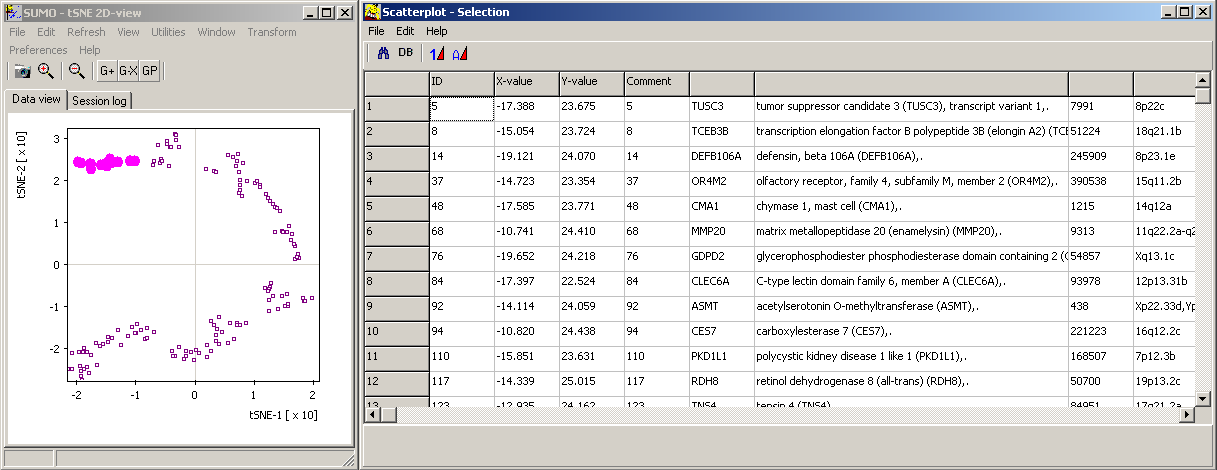
You may also load addtional values for the data points (e.g. regulation, intensity, ...) and show them as indivdual data point's color, size (Scatterplot main menu | Paste data | Size/Color.
But take care that pasted data have exactly same order and size as map data.
See more details about Scatterplot viewer.


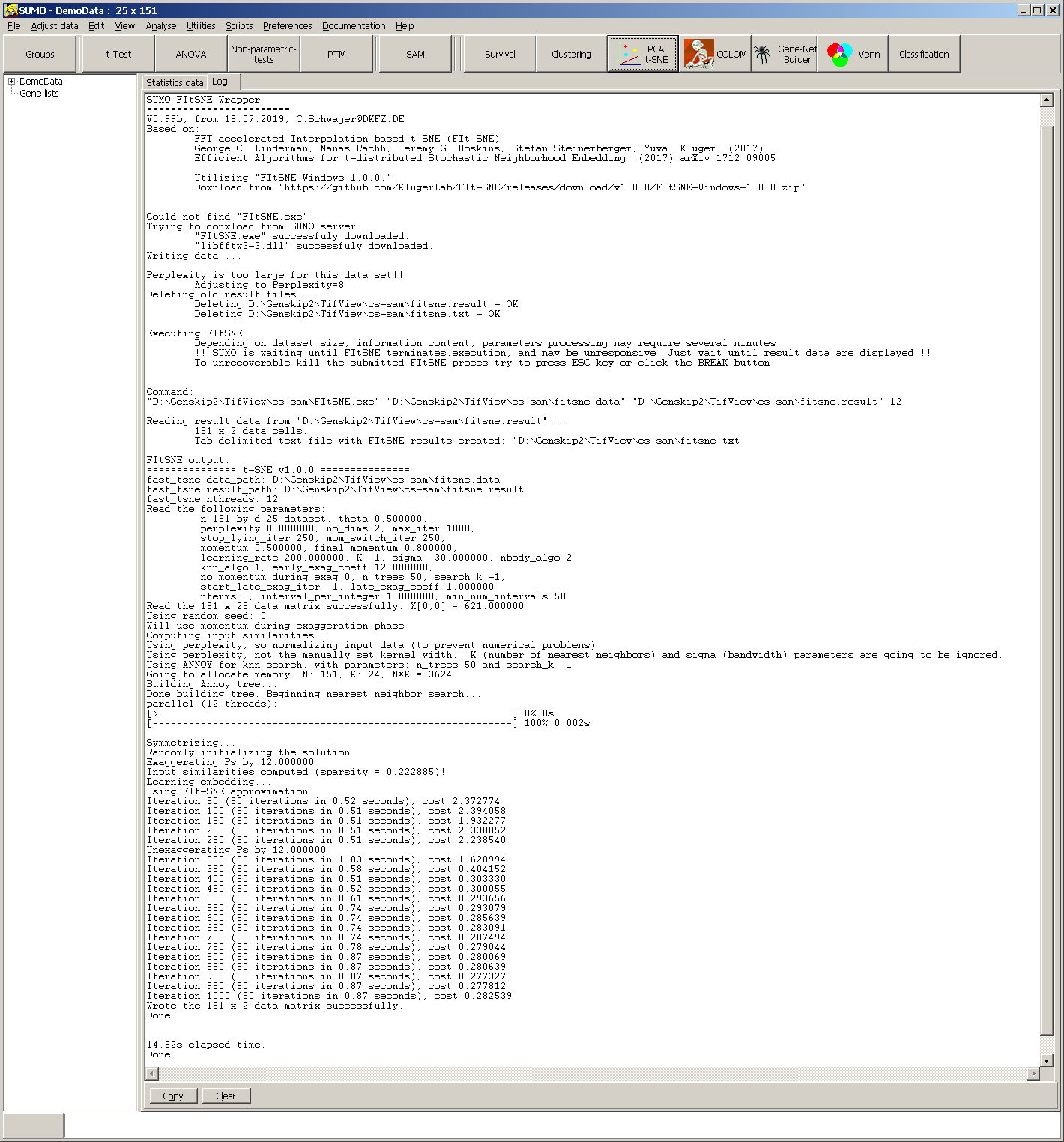
Finally the process-report as well as an error-report (if errors occurred) from FItSNE is shown in the message/Log tabshet:
In case the tSNE mapping is not informative, this processing output may contain hints how to adjust FIt-SNE parameters.










UMAP

In a first step, UMAP computes similariteis between all data vectors (using distance metrics well known from hierarchical clustering) and filters most relevant interactons.

In a second step these interactiosn are embedded in 1-/2-/3-D space applying a "force-feed" method similar to network building (e.g. gene-networks).

For more details about UMAP see:

     Leland McInnes, John Healy, James Melville.
     UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction
     arXiv:1802.03426 [stat.ML]

or a basic introduction into UMAP including several samples on GitHub.

SUMO does not use an own implementation of UMAP but wraps the Python based implementation from      Leland McInnes, John Healy, James Melville.

This requires installation of Python, the UMAP package as well as any additional underying Python packages imported by UMAP.

We recommend to install Python / UMAP via ANACONDA / Miniconda.



Installation of ANACONDA

Goto to distribution site and download a suited Windows installer version for your system (e.g. Anacoda 2019.10, Windows Installer, Python 3.7 version, 64-Bit Graphical Installer.)

During installation you may select between installation only for the current or for all users:
  • Current user - no administrator account required for installation.
    Install outside a Windows user account's folders (NOT: Deskttop, Own documents, ...) but on a public avialable folder (e.g. second data drive).
    Thus the installation of ANACONDA may be used by any user on this computer.
    Other user must create links to ANCONDA on their own.
  • All users - Install by adminsitrator. All users of this computer may access ths ANACONDA installation.



Install UMAP

After successful installation of ANACONDA open an ANACONDA prompt fron Windows's start menu.

Install UMAP by typing:

conda install -c conda-forge umap-learn

or

conda install -c conda-forge/label/cf201901 umap-learn

ANCONADA now will download UMAP as well as all other required Python packages.



Setup ANACOND Proxy server:

In case your computer system accesses the Internet via an institutional proxy server, installation may fail.
Then it may be necessary to tell ANACONDA about this proxy prior to installation of new packages.

See here how to configure ANACONDA.

In brief:
  • Use a text editor (eg. Windows' notepad.exe) to create a configuration file in your users home directory:
    E.g. "c:\users\myAccount\.condarc"
    Replace "myAccount" with the respective user account name.
    ".condarc" MUST be used, don't forget the leading "."

  • add the proxy definition:

    
proxy_servers:
  http: http://user:pass@corp.com:8080
  https: https://user:pass@corp.com:8080

    Replace "corp.com" with the name of your organisation's proxy server
    Replace "8080" with your organisation's proxy port number
    If your organisation's proxy requires authentication replace "user:pass" with your username:password
    If your organisation doesn't require proxy authentication - skip user:pass

  • Save the file.
    Now ANACONDA should be able to access its repositories for software installation.



UMAP with SUMO

Load a data matrix.

Click the PCA / t-SNE / UMAP-button or select Main menu | Analyses | PCA / t-SNE / UMAP.

Select to run a UMAP analysis with either Genes (row-vectors) or Conditions (column vectors).

A parameter dialog opens up, allowing to set UMAP processing parameters:


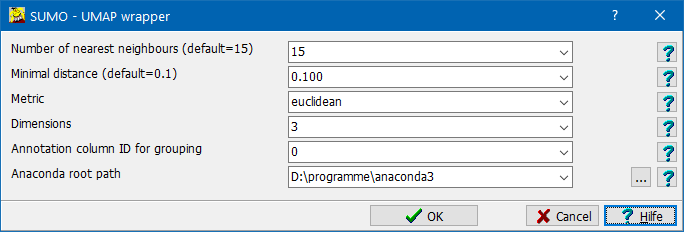
Number of nearest neighbors
Minimal distance

Dimensions: Define number of dimensions for embedding:
1 - dimensioanl embedding
2 - dimensional embedding => data clouds in a 2D-plain (commonly used model)
3 - dimensional embedding => data clouds in a 3D-space
Metric Method how to compute similarity / distance between data vectors.
Choice of a metric may fudamentally alter resulting embedding.
Thus consider carefully which metric to use depending on the data, the experimental design and the scientific question.
Annotation column ID
for grouping		 Data viewers will use this annotation column to auto group (genes/conditions).
The annotation column should contain a small set (~≤<100) of "class identifiers" (e.g. treatment names).
Specify "0" or leave empty to avoid autogrouping.
Anaconda path Specify location of your ANACONDA, or any other Python installation
Click the  ...  button to open a file system browser and navigate to the repective folder.

Click the  OK  button to lauch UMAP.

SUMO performs the steps:
  • Write processing parameters and data into a Comma Separated Values file (.csv).
    A file ("SUMO_umap_data.csv") is created in the folder were SUMO.exe is located.

  • Generate a Python script to perform UMAP analysis.
    A file ("SUMO_umap.ps") is created in the folder were SUMO.exe is located.

  • Create a Windows command script to set the ANACONDA environment and launch the analysis.
    A file ("SUMO_umap.bat") is created in the folder were SUMO.exe is located.

  • Wait until UMAP has finalised.
    Although in principle possible, it may be wise not to run other SUMO functionality while waiting for UMAP to finalize.
    You may terminate UMAP at any time by pressing ESC-key or clicking the  Break  button.

  • Load and display results as 2D-/3D-scatterplots
    Data are read from TAB-delimited result ("SUMO_umap_resut.txt") file created by the "SUMO_umap.ps" Python script.

  • Info / Error-Messages from the scripts / UMAP / Python are show in SUMO's Log tab-sheet.



SUMO generates a UMAP specific data file, saves it in the folder where SUMO executable reside, und starts UMAP.

UMAP requires numeric data - obvious.
Thus, you should impute non-numeric values in your data matrix prior to running UMAP.
In case /SUMO finds non numeric values while writing the UMAP data file, it will finally replace NANs by ZERO.
In case of very few randomly distributed NAN cells, this will most probably have low iimpact on the embedding.
Larger number of NANs concentrated in singular data rows/columns or even correlating with data structures may introduce biases and thus artificial mappings.

Depending on data size (i.e. number of data vectors, length of data vectors) and internal data structure, UMAP may require a while to process the data.

Some timings with random data, I7-8700k, 3.4 GHZ, 12 hyperthreads, 64 GB RAM:

Number of   
vectors		Legth of   
vectors		Elapsed   
time
(s)
1001005.27
10001007.63
1000010031.67
100000100171.53
10010006.11
1001000011.83
10010000068.28

Thus, be patient and wait until UMAP has finalized.



Like with any othe similarity based data partitioning method, unspecific background signals or very low intensity noisy data may - in the best case - not be helpful for embedding but only consume CPU time.
In the worse case they can introduce biasis which may even generate meaningless sub-structures in the final embedding.



Some samples:

Graphs are generated from SUMO's internal "Intensity" demo data set, applying UMAP to genes:
1-D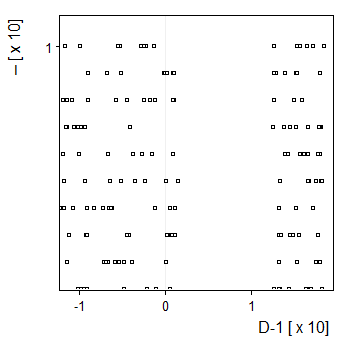

Here, Y-Dimension is meaningless.
 2-D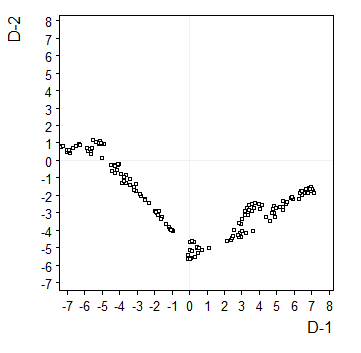

 
 3-D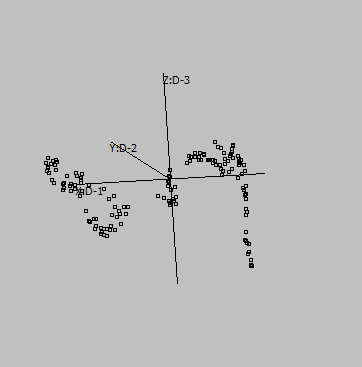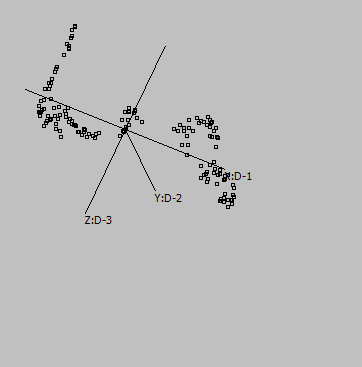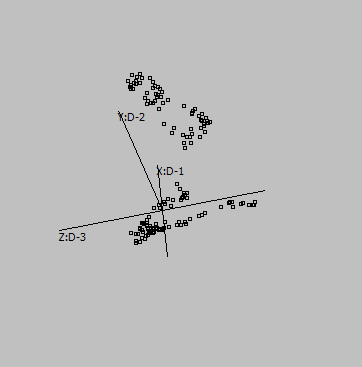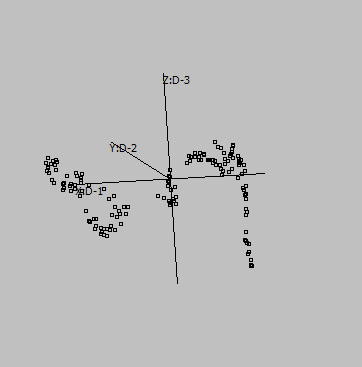

 

Embeddings in different dimensions may suggest different sub-structures.

Embedding parameters may influence the embedding, e.g. metric:

Euclidean

 
 Canberra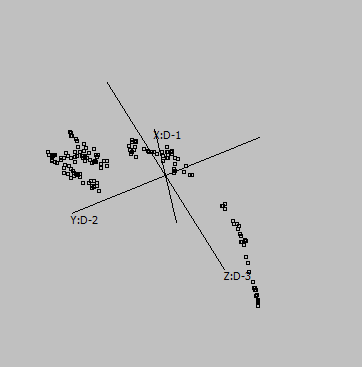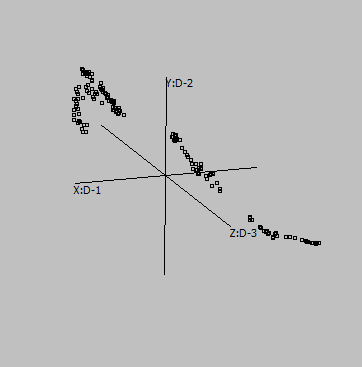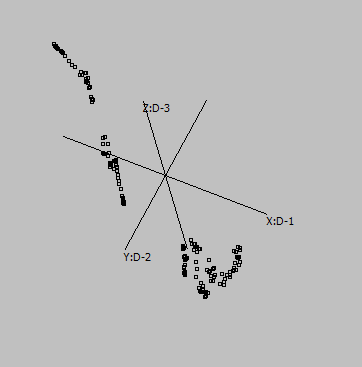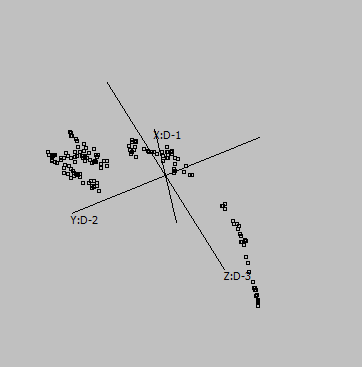

 
 Cosine

 
 Correlation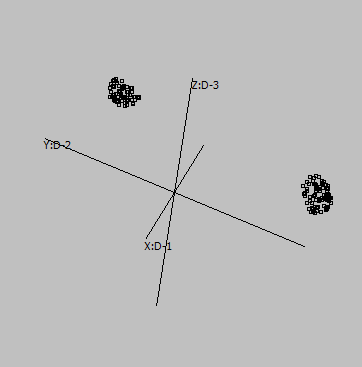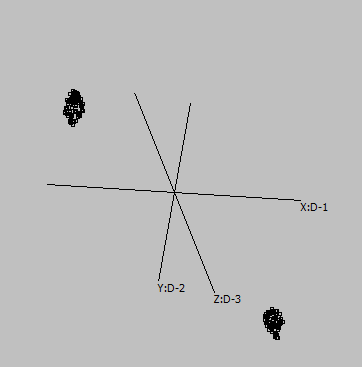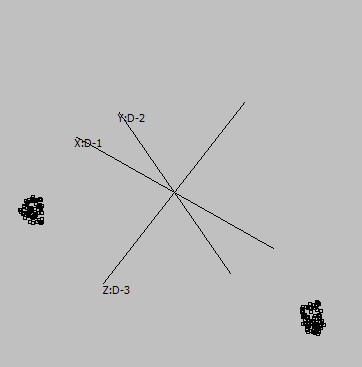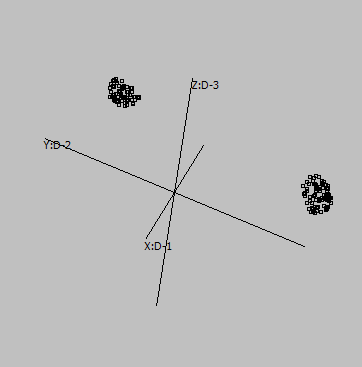